Brilliant Strategies Of Info About How To Build A Pda

$$ now combine the two pda's for the language $$ \{0^n1^m :

How to build a pda. Pushdown automata is a way to implement a cfg in the same way we design dfa for a regular grammar. A dfa can remember a finite amount of information, but a pda can. I saw in a book how to construct a pda for a case with m is equal to n.

Pdas are created by hashing a number of seeds the user can choose and the id of a program: But finite automata can be used to accept only regular languages. There are two use cases for pdas.

Each transition is based on the current input symbol and the top of. Here, take the example of odd length palindrome: It's pretty simple, just push a symbol for every a and pop this symbol for every b that the.

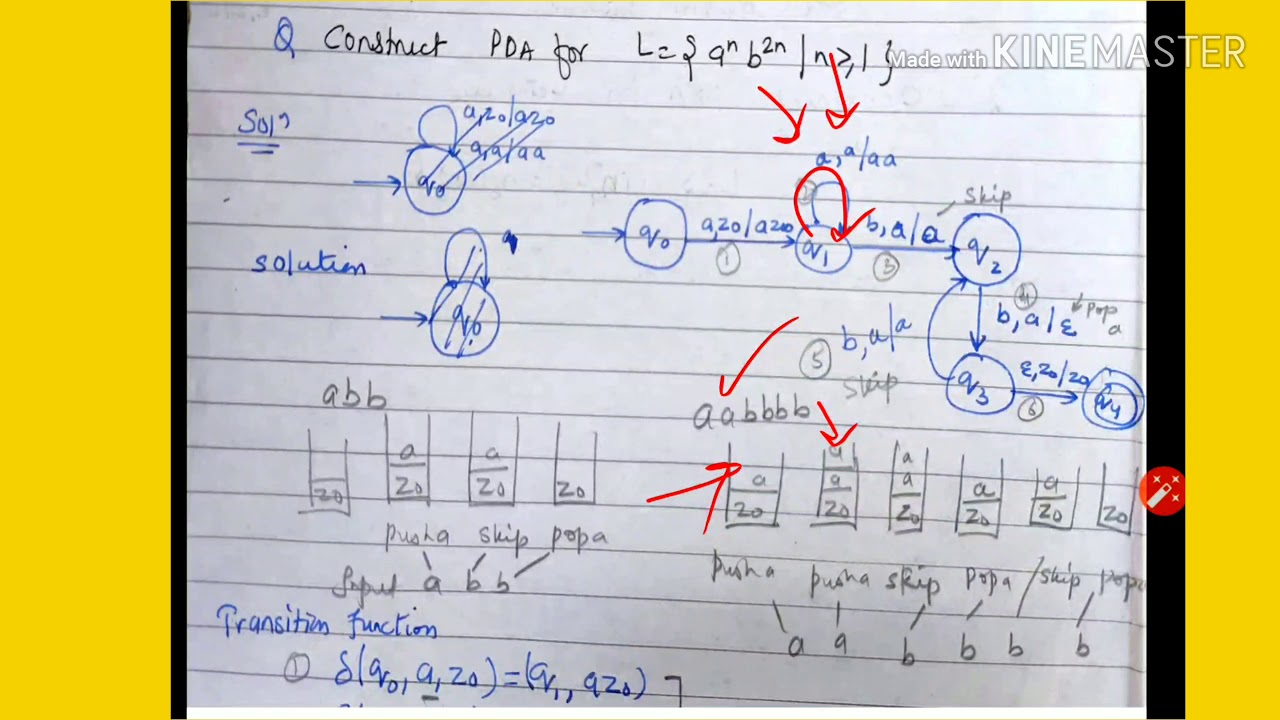
Hence, it is important to learn, how to draw pda. 654k views 3 years ago toc (theory of computation) 👉subscribe to our new channel: We can easily make a pda that accepts a^n b^n, and we can easily make one that accepts a^n b^2n.

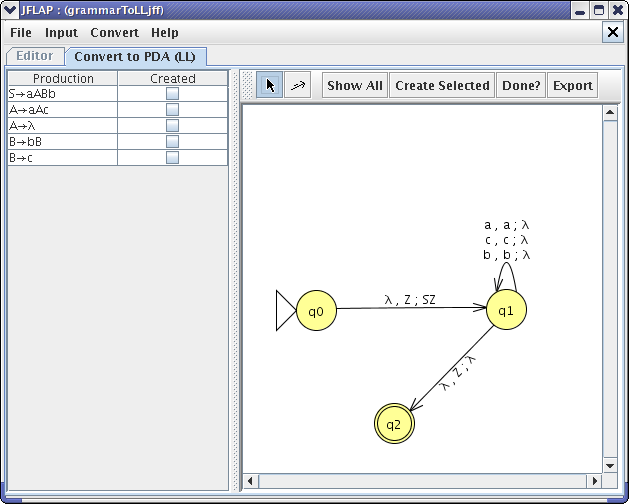
Try to construct two pda's for languages given below $$ \{0^n1^m : Conversion of cfg to pda consists of five steps. Cfg to pda conversion.

Convert the cfg productions into gnf. The seeds can be anything. There will only be one.

The steps are as follows: / @varunainashots in this video design pda for 0^n1^2n cfl language is discussed. Pushdown automata is a finite automata.

N > m\}, \quad \{0^n1^m : Read video we have already discussed finite automata. If we need to use pda acceptance by final state then two states are required as we need a working state and a separate accepting state.

// pseudo code let pda = hash(seeds, program_id); Construct a pda for the language l = { w = x1y1x2y2….xnyn | where w belongs to {0,1}*, and the string y1y2….yn is the same as x1x2….xn except the 1’s in y.